Filtres analogiques passifs -

Filtres analogiques passifs

Dans le domaine du traitement numérique du signal, les filtres sont des éléments qui suppriment (ou, plus exactement atténuent) certaines fréquences contenues dans une forme d’onde.

Par exemple, prenons une fréquence basse de 1 KHz (amplitude 5V)

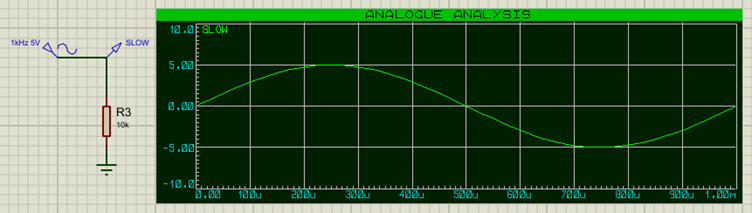
Et une fréquence plus rapide de 50KHz (amplitude 1V) :

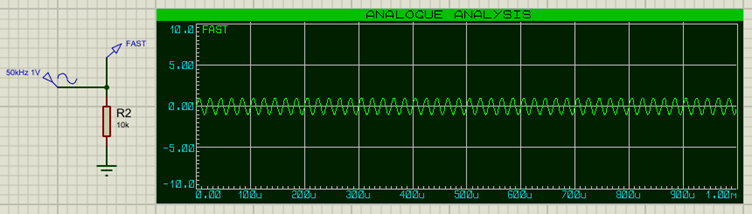
Le signal combiné de ces deux fréquences ressemble à ceci :

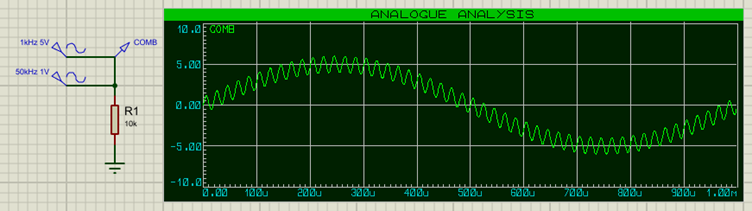
Les générateurs de Proteus peuvent être initialisés en source de tension ou de courant. Pour sommer les deux générateurs de 1kHz et 50kHz nous les utilisons en source de courant comme montré ci-dessous relativement au signal sinusoidal de fréquence 50KHz!

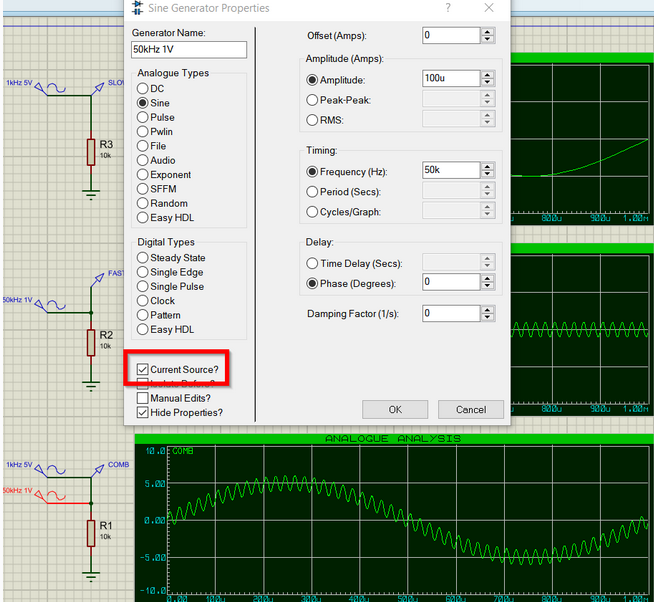
Grâce à l’utilisation de filtres, nous pouvons décomposer le signal combiné, par filtrage, afin d’en extraire les différentes composants. Pourquoi faire cela ? Il existe de nombreuses raisons telles que :

Partager le medium

Dans le cas d’ondes radios (Wifi, téléphone mobile, etc) tous les signaux partagent le même canal de transmission. C’est comme s’il n’existait qu’un fil de communication partagé entre tous. Le fait d’utiliser des fréquences différentes, permet à plusieurs utilisateurs de partager le medium et de filtrer les fréquences pour ne s’intéresser qu’à certaines.

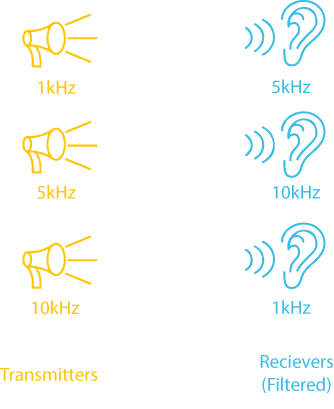
Medium partagé

2. Bruit

Le bruit peut être induit dans un signal par plusieurs sources, par exemple une interférence électromagnétique. Il est possible de supprimer ce bruit par filtrage.

Voyons comment nous implémentons des filtres.

Composants réactifs

Dit simplement, les composants réactifs sont des composants dont le comportement varie en fonction de la fréquence qui leur est appliquée. En électronique il existe deux types de composants réactifs, qui sont les condensateurs et les inductances. Les deux types de composants emmagasinent l’énergie dans un champ magnétique. Les condensateurs stockent l’énergie en accumulant des charges entre deux plaques.

Lorsqu’une tension est appliquée au condensateur alors un courant y circule jusqu’à ce que la tension entre les plaques corresponde à la tension appliquée. A ce stade, l’énergie est stockée dans les charges accumulées sur les plaques. Les charges sont maintenues en place grâce à l’attraction magnétique entre elles. Lorsque le condensateur est chargé, le courant s’arrête de circuler jusqu’à ce que la tension soit supprimée, ce qui permet au courant de circuler à nouveau.

Ainsi nous voyons que le courant circule lorsque la tension évolue et s’arrête de circuler lorsque la tension est constante ; lorsqu’il n’y a pas de différence de tension, aucun courant ne circule. Il semble contre intuitif qu’un courant puisse circuler dans un condensateur en mode DC, car il n’y a pas de connexion entre les plaques du condensateur ; cependant un courant AC peut y circuler car l’énergie est transférée via le champ magnétique interne au condensateur. Dans une optique AC, le condensateur bloque les basses fréquences alors que les hautes fréquences peuvent circuler.

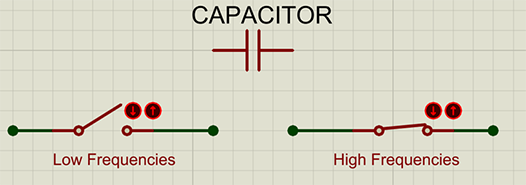
Aux basses fréquences, le condensateur ressemble à un circuit ouvert. Aux fréquences hautes, le condensateur est un court-circuit. Entre les deux, le condensateur est équivalent à une résistance qui s’oppose au passage du courant. La spécificité d’un condensateur, c’est qu’il ne dissipe pas l’énergie en chaleur comme une résistance, mais la stocke dans son champ magnétique.

Les inductances, quant à elles, stockent l’énergie dans le champ magnétique qui se développe autour des spires.

Contrairement aux condensateurs, les inductances permettent au courant d’y circuler lorsque la tension ne change pas, et s’opposent à des changements de courant et de tension. Alors que les condensateurs ressemblent plus à un élastique, les inductances font penser à une roue libre (voir les articles sur les convertisseurs ‘boost’ et ‘buck’). Lorsqu’une tension est appliquée à une inductance, initialement elle s’oppose à la circulation de courant pendant l’établissement d’un champ magnétique autour de ses spires. Une fois établi, le courant DC traverse l’inductance sans entrave. Si vous tentez d’arrêter le passage du courant, alors le champ magnétique produit une tension qui tente de préserver la circulation du courant.

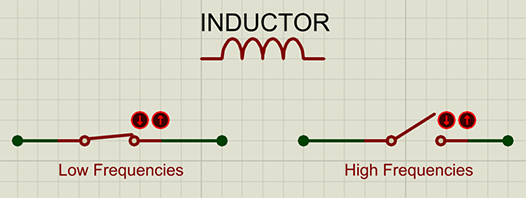
Aux basses fréquences, le condensateur ressemble à un court-circuit. Aux fréquences hautes, le condensateur est comparable à un circuit ouvert. Entre les deux, une inductance est équivalente à une résistance qui s’oppose au passage du courant. La spécificité d’une inductance, c’est qu’elle ne dissipe pas l’énergie en chaleur comme une résistance, mais la stocke dans son champ magnétique.

Avec les condensateurs et les inductances, nous disposons de deux éléments réactifs, de comportement opposé par rapport à des fréquences AC. Nous pouvons utiliser ces propriétés pour construire des filtres avec ces composants.

Décibels

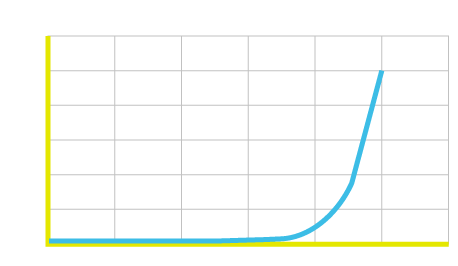
Avant d’aller plus loin, il est important de comprendre l’unité de mesure appelée décibel. C’est une unité logarithmique illustrée dans le graphe qui suit :

20dB signifie 10 x l’amplitude et 100 x la puissance, 40dB signifie 100 x l’amplitude et 10000 x la puissance, et ainsi de suite (nous n’indiquerons par ici la relation entre l’amplitude AC et la puissance AC).

Il suffit de dire que le calcul de la puissance AC est plus complexe que la puissance DC donnée par P = V x I. Les décibels (dB) sont une unité de mesure qui nous permet de travailler facilement depuis de très faibles valeurs vers des très grandes, et rend les calculs très simples pour une chaîne de systèmes car les dBs s’additionnent.

Graphe de réponse en fréquence

Le graphe de réponse en fréquence ou diagramme de Bode montre la réponse d’un circuit en fonction de la fréquence. Il est donc particulièrement adapté à la conception et l’analyse des filtres comme nous allons le voir dans les prochaines sections.

Le filtre passe-haut

Ce filtre permet aux fréquences hautes de le traverser, alors que les basse fréquences sont atténuées (bloquées). Comme nous l’avons vu, les condensateurs admettent les hautes fréquences, c’est pourquoi nous utiliserons ces composants pour construire un filtre passe-haut.

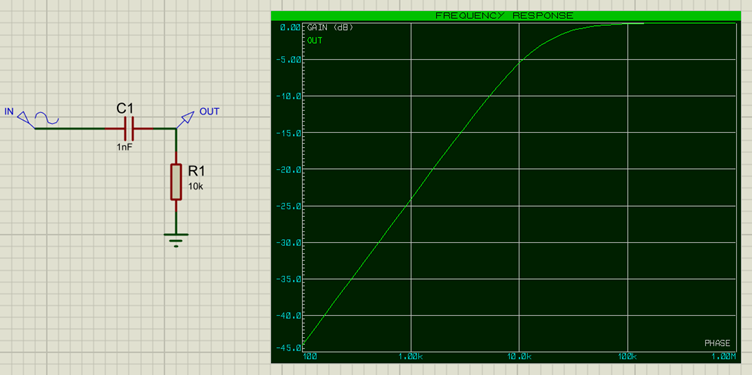
Le graphe de réponse en fréquence montre que les fréquences supérieures à 16k sont admises (proches de 0dB), alors que les fréquences plus basses sont atténuées de plus en plus (à 100 Hz, l’atténuation est de -44 dB) . Le filtre n’est pas un mur de brique qui bloque toutes les fréquences mais plutôt les atténue de plus en plus lorsque la fréquence diminue. Nous pouvons augmenter l’atténuation en combinant des filtres, ce qui augmente l’ordre du filtre.

Super ! Essayons cela avec notre exemple initial :

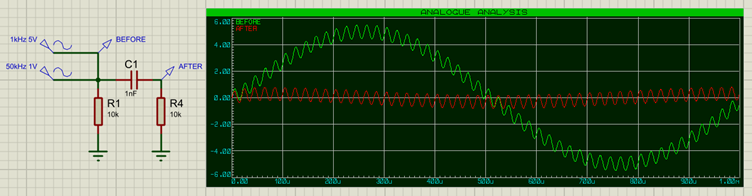
Nous voyons que la fréquence de 1 KHz est pratiquement éliminée du signal après le condensateur (courbe rouge du graphe). Nous verrons plus loin comment calculer la valeur des composants pour une fréquence donnée.

Le filtre passe-bas

Le filtre passe-bas est l’opposé du filtre passe-haut et permet aux fréquence basses de passer tout en atténuant les fréquences hautes. Pour modifier notre exemple, il suffit de remplacer le condensateur par une inductance :

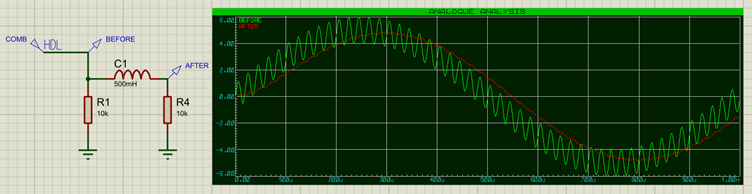
Dans ce cas, la fréquence haute de 50 kHz est pratiquement supprimée du signal après la passage par l’inductance (courbe rouge du graphe). Le graphe de réponse en fréquence pour l’inductance ressemble à celui-ci :

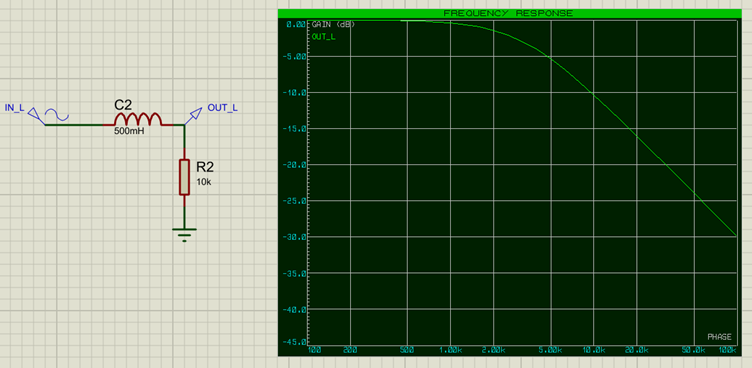
Les fréquences plus basses que 3k passent (proche de 0dB) alors que les fréquences supérieures sont de plus en plus atténuées (à 100kHz, l’atténuation est de -30dB). Ici aussi, il est possible de combiner des filtres pour améliorer l’atténuation.

Nous pouvons aussi construire un filtre passe-bas avec un condensateur :

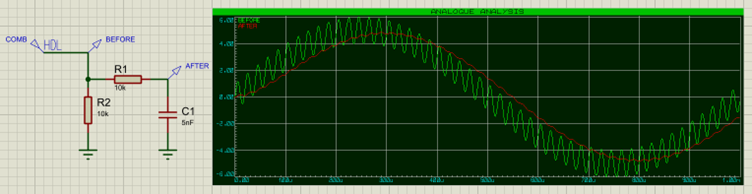
Dans ce cas les hautes fréquences passent au travers le condensateur vers la masse. Le graphe correspondant ressemble à ceci :

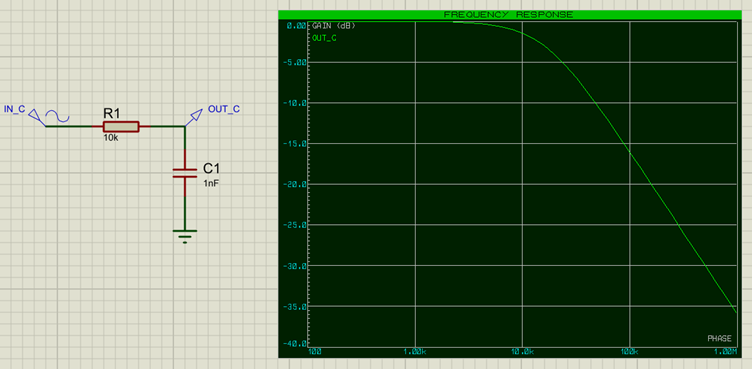
Autre filtre passe-haut

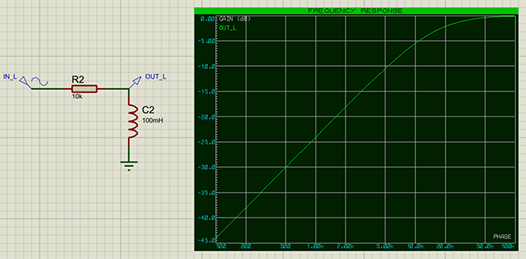
De la même manière nous pouvons construire un filtre passe-haut avec une inductance :

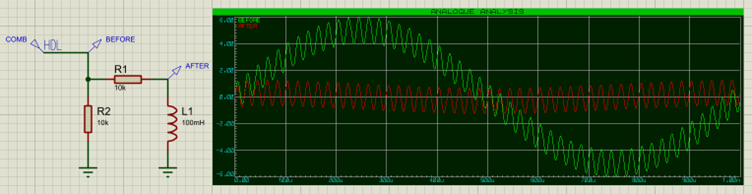
Dans ce cas, ce sont les basses fréquences qui traversent l’inductance vers la masse. Le graphe correspondant ressemble à ceci :

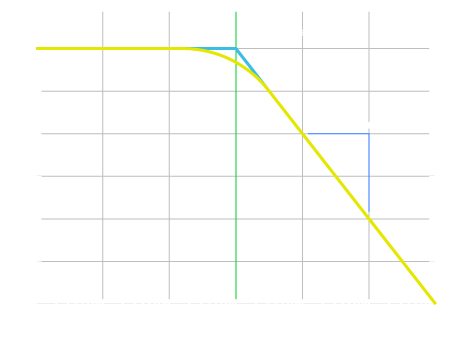
La fréquence de coupure

La fréquence de coupure correspond au point à – 3dB du graphe de réponse en fréquence. C’est le point pour lequel le signal est atténué de 50% par rapport à la puissance d’origine (approximativement 70.8% de la tension d’origine). C’est aussi le point de rencontre des lignes d’atténuation de de passage du signal.

La fréquence de coupure est donnée par la formule :

Cutoff Frequency = 1 / 2πRC

pour un filtre capacitif. Pour un filtre inductif, c’est :

Cutoff Frequency = R / 2πL

Utilisons ces formules avec la valeur des composants de nos graphes de réponse plus haut. Dans le cas du filtre capacitif, nous avons une résistance de 10k avec un condensateur de 1nF, ce qui donne :

Cutoff Frequency = 1/2π(10×10³)(1×10-9) = 15.9kHz

Pour le filtre inductif, nous avons une résistance de 10k avec une inductance de 100mH :

Cutoff Frequency = (10×10³)/2π(0.1) = 15.9kHz

Dans le deux cas, nous voyons que les valeurs correspondent à celles de graphes.

Filtres d’ordre plus élevés

Tous les filtres que nous avons présenté contiennent un seul élément réactif. La pente des graphes de réponse est d’environ 10dB/décade logarithmique. En utilisant plus d’éléments réactifs et/ou en associant des filtres nous pouvons augmenter la pente de 20dB par élément réactif. On dit que l’ordre du filtre augmente. Par exemple, ci-dessous nous présentons un filtre du deuxième ordre (2 éléments réactifs) avec une pente de 40dB/décade.

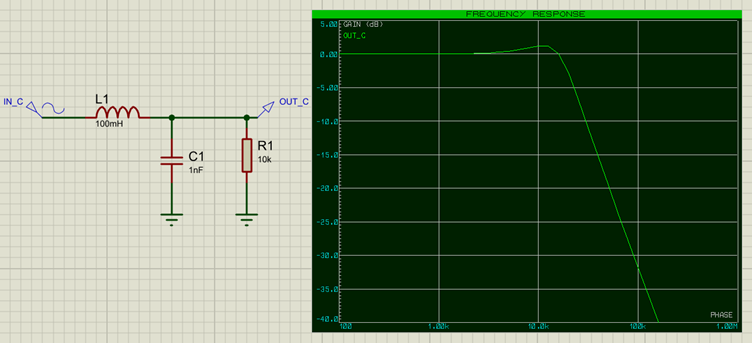
Notez cependant qu’il y existe des inconvénients à trop incrémenter l’ordre du filtre car cela fait varier l’atténuation du signal dans la bande passante et ajoute un retard de propagation. De plus la complexité du circuit augmente ainsi que son coût.

Filtres passe-bande et coupe-bande

Il est également possible de créer des filtres passe-bande ou coupe-bande par une combinaison de filtre passe-haut et passe-bas avec des fréquences de coupure appropriées.

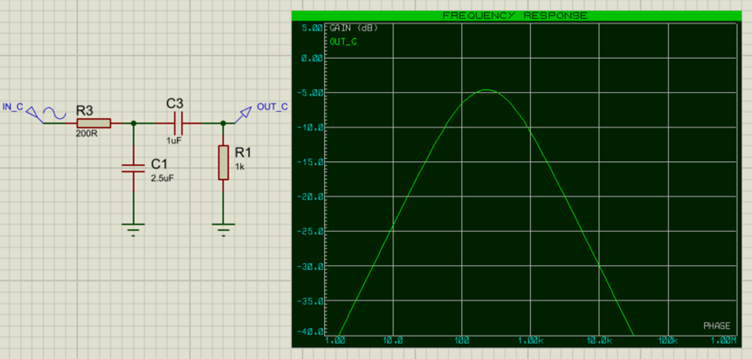
Conclusion

Les filtres sont des modules assez simples à comprendre et représentent des outils essentiels en traitement du signal, à connaître par tout ingénieur. Dans cet article nous nous sommes concentrés sur la filtres analogiques passifs ; il existe également des filtres analogiques actifs que nous aborderons dans un autre article.

Tous les exemples et les graphes de cet article ont été créés avec la suite Proteus. Le module de simulation avancée par graphes dispose de douze types de graphes différents avec la possibilité d’inclure des générateurs de signaux ainsi que des sondes de tension/courant.

Traduction française