Les ADC à approximations successives
Introduction
Les convertisseurs analogiques-numériques (CAN), ou ADC (de l’anglais « Analogue to Digital Converters »), convertissent une tension analogique en un nombre numérique (utilisé dans un ordinateur, tel qu’un microcontrôleur). Les CAN ont une résolution particulière, ainsi qu’une tension de référence positive et négative. Un ADC de 10 bits, par exemple, convertit la tension d’entrée en un nombre compris entre 0 et 1023 (1023 étant le plus grand nombre pouvant être représenté avec 10 bits). Si la tension de référence négative est de 0V et la tension de référence positive est de 5V, alors un résultat ADC de 0 signifierait 0V, et un résultat ADC de 1023 signifierait 5V. Un résultat ADC de 511 signifierait 2,5V, et ainsi de suite. Chaque pas numérique (la résolution) serait équivalent à environ 4,9 mV (5V/1024).

Un exemple de copie de données de la mémoire vers un périphérique est le cas où une grande quantité de données doit être transmise via un périphérique de communication (tel qu’un UART). Sans DMA, le CPU devrait soit se « bloquer » pendant la transmission des données (ce qui se ralentirait généralement la transmission en fonction de la vitesse du protocole de communication), soit utiliser des interruptions pour gérer la transmission (ce qui ajouterait des traitements supplémentaires liés à la commutation de contexte d’interruption).
Cet exemple ne prend en compte que le cas où il n’y a qu’une seule transmission de données qui doit se produire simultanément. En règle générale, le DMA peut traiter plusieurs flux de données en même temps (selon l’implémentation particulière du microcontrôleur).
Pour plus d’information sur les signaux analogiques et numériques, voir notre article dédié à ce sujet.
Il existe plusieurs types de convertisseurs analogiques-numériques (CAN), et dans cet article, nous examinerons le Convertisseur à Approximations Successives [Register] ou SAR ADC. Les SAR ADC sont le type le plus couramment rencontré dans les microcontrôleurs et offrent un temps de conversion rapide (latence faible) pour des résolutions typiques.
Anatomie d'un SAR ADC
Les SAR ADC se composent de 3 composants principaux :
- Circuit d’échantillonnage et de maintien.
- Convertisseur numérique-analogique (DAC – Digital to Analog Converter).
- Comparateur.
(Le registre d’approximation successive lui-même, qui pilote le DAC, peut être considéré comme un 4e composant)

Vous pouvez également consulter notre article sur les amplificateurs opérationnels (qui incluent des comparateurs) et les DACs avant d’aller plus loin.
Le circuit d’échantillonnage et de maintien prend un échantillon de la tension d’entrée, puis le stocke (le maintenant constant et stable) pendant que la conversion est effectuée. Conceptuellement, il s’agit simplement d’un interrupteur et d’un condensateur ; l’interrupteur se ferme pour charger le condensateur à la tension d’entrée, puis s’ouvre à nouveau pour laisser le condensateur maintenir la tension échantillonnée.
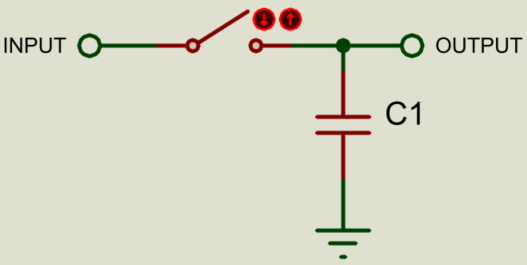
En pratique, certains amplificateurs opérationnels tampons (voir notre article sur les amplificateurs opérationnels) sont utilisés pour éviter la distorsion des tensions.
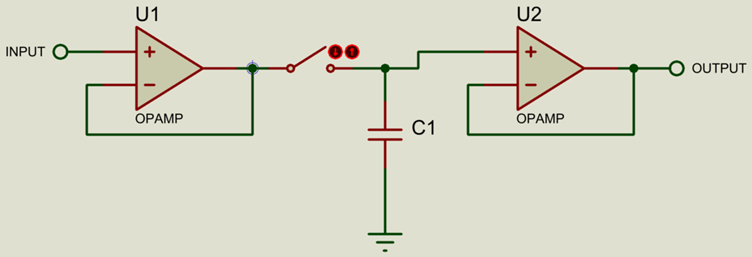
L’interrupteur est mis en œuvre via un transistor.
En utilisant le DAC et le comparateur, une recherche binaire est ensuite effectuée pour approximer la valeur de l’entrée.
Recherche binaire
Une recherche binaire est un type d’algorithme de recherche qui affine les résultats en divisant continuellement le domaine de recherche par 2 (binaire) et en vérifiant de quel côté du domaine de recherche se trouve l’entrée. Autrement dit, l’algorithme vérifie si l’entrée est supérieure ou inférieure à la valeur au milieu du domaine de recherche. Cela est peut-être plus facile à expliquer avec un exemple :
Supposons que nous ayons un ensemble de nombres, triés du plus petit au plus grand, et que nous devions insérer un autre nombre dans l’ensemble tout en le maintenant trié. Comment l’ordinateur déterminerait-il où insérer le nombre ?
Insérez le nombre 55 dans l’ensemble suivant, en maintenant l’ordre du plus petit au plus grand.
Une méthode consiste simplement à commencer au début de l’ensemble, à inspecter chaque nombre un par un jusqu’à ce que nous trouvions un nombre plus grand que notre entrée (ou jusqu’à ce que nous atteignions la fin de l’ensemble), puis à insérer le nombre juste avant celui-ci. Cette méthode peut être assez rapide pour de plus petits ensembles de nombres, mais à mesure que la taille de l’ensemble augmente (jusqu’à des centaines et des milliers d’entrées), un algorithme de recherche sera généralement beaucoup plus rapide.
En utilisant l’algorithme de recherche binaire, nous divisons le domaine de recherche par 2, puis nous vérifions si notre entrée est plus grande ou plus petite que le nombre au milieu. Comme il n’y a pas exactement un milieu, nous mettons en place une règle qui dit que nous utilisons le nombre juste à droite du milieu :
55 > 40, donc nous réduisons notre recherche à la partie supérieure du domaine de recherche, et répétons :
55 < 77, donc nous réduisons notre recherche à la partie inférieure du domaine de recherche révisé :
55 > 45, donc nous savons que le nombre se situe juste à droite de 45 pour cet ensemble.
Pour un ensemble de 8 nombres, ce processus prendra toujours un total de 3 étapes de recherche.
SAR ADC Binary Search
La recherche binaire du SAR ADC fonctionne de la même manière, en utilisant le DAC pour générer l’ensemble de nombres à rechercher et le comparateur pour comparer la valeur d’entrée à la position de recherche actuelle.
Supposons que nous ayons un ADC de 4 bits, offrant une résolution de 16 étapes (valeurs de 0 à 15), une tension de référence positive de +5V (tension de référence négative de 0V) et une tension d’entrée de 3,6V.
Nous commençons avec une valeur binaire de 1000 dans le registre d’approximation successive, ce qui est 8 en décimal (juste au-dessus de la moitié).

La tension de sortie du DAC est alors de 2,67V (8 / 15 x 5V). Le comparateur vérifie et constate que l’entrée de 3,6V > 2,67V, donc nous laissons le Bit 3 à 1 et passons au Bit 2, que nous définissons également à 1 (nous mettons toujours le bit suivant à 1 lorsque nous passons à celui-ci).
Supposons que nous ayons un ADC de 4 bits, offrant une résolution de 16 étapes (valeurs de 0 à 15), une tension de référence positive de +5V (tension de référence négative de 0V) et une tension d’entrée de 3,6V.
Nous commençons avec une valeur binaire de 1000 dans le registre d’approximation successive, ce qui est 8 en décimal (juste au-dessus de la moitié).

La sortie du DAC est maintenant de 4V, donc le comparateur vérifie et constate que l’entrée de 3,6V < 4V, donc nous mettons le Bit 2 à 0 et passons au Bit 1, en le réglant également à 1.

La sortie du DAC est maintenant de 3,33V, donc le comparateur vérifie et constate que l’entrée de 3,6V > 3,3V, donc nous laissons le Bit 1 à 1 et passons au Bit 0, en le réglant également à 1.

La sortie du DAC est maintenant de 3,67V, donc le comparateur vérifie et constate que l’entrée de 3,6V < 3,67V, donc nous mettons le bit 0 à 0 et la conversion est maintenant terminée.

Une entrée de 3,6V sur un ADC de 4 bits avec une tension de référence positive de +5V (et une tension de référence négative de 0V) se convertit en une valeur binaire de 1010 (décimale 10).
D’un autre point de vue, ce processus ressemble à ce qui suit :
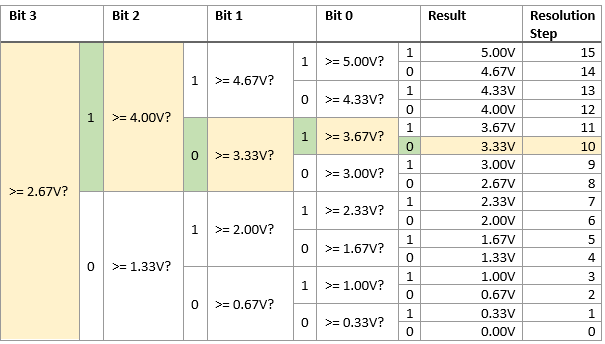
Voici un autre exemple pour une tension d’entrée de 1.10V :
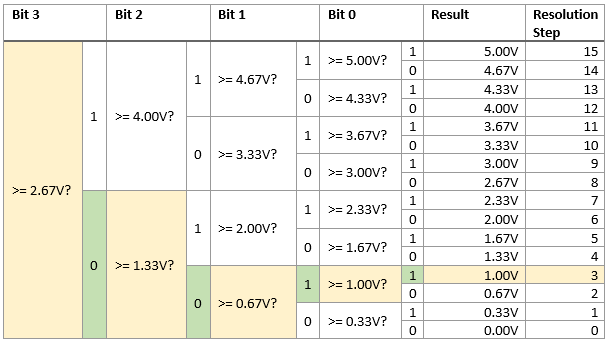
Notez que l’algorithme de recherche binaire se termine toujours en un nombre fixe d’étapes, ce qui signifie qu’il met toujours le même temps pour exécuter la conversion.
Résumé
Les SAR ADC (convertisseurs analogiques-numériques à registre d’approximation successive) sont un type populaire de convertisseur analogique-numérique, offrant un temps de conversion relativement rapide pour des résolutions typiques. En raison de l’algorithme de recherche binaire utilisé par ces ADC, qui prend toujours un nombre fixe d’étapes, le temps de conversion est prévisible.
Copyright Labcenter Electronics Ltd. 2024
Traduction française
Copyright Multipower France 2024
