Les systèmes de numération -

Les systèmes de numération

Introduction

Nous savons tous compter ! Mais savez vous compter en binaire ou en hexadécimal ? Ainsi que additionner, soustraire, multiplier et diviser dans un système de numération différent ?

Nous tenons pour acquis que nous travaillons exclusivement avec un système de numération en base 10 (décimal) jusqu’au jour où nous rencontrons un système différent (tel que le binaire ou l’hexadécimal). Cependant, la réalité est que le système familier en base 10, qui nous sert au quotidien, est totalement arbitraire et probablement lié à nos 10 doigts (pour compter). D’autres systèmes de numération sont tout autant valides !

Base 10 signifie qu’il existe 10 valeurs possibles pour chaque chiffre.

Lorsque toutes ce valeurs possibles ont été parcourues, on ajoute un autre chiffre.

Et ainsi de suite..

Nous admettons ce mécanisme appris pendant l’enfance. Voyons comment il peut être adapté à d’autres systèmes de numération.

Binaire

En interne, les ordinateurs utilisent des commutateurs (transistors) qui n’ont que 2 états possibles : On et Off. Ceci signifie qu’il n’existe que 2 valeurs possibles (0,1) pour chaque chiffre (digit) dans le monde des ordinateurs. Pour compter en binaire les mêmes règles s’appliquent – lorsque toutes les valeurs possibles pour un digit ont été parcourues, il faut ajouter un nouveau digit.

Voici un tableau pratique qui permet de comparer le système base 2 au système base 10 :

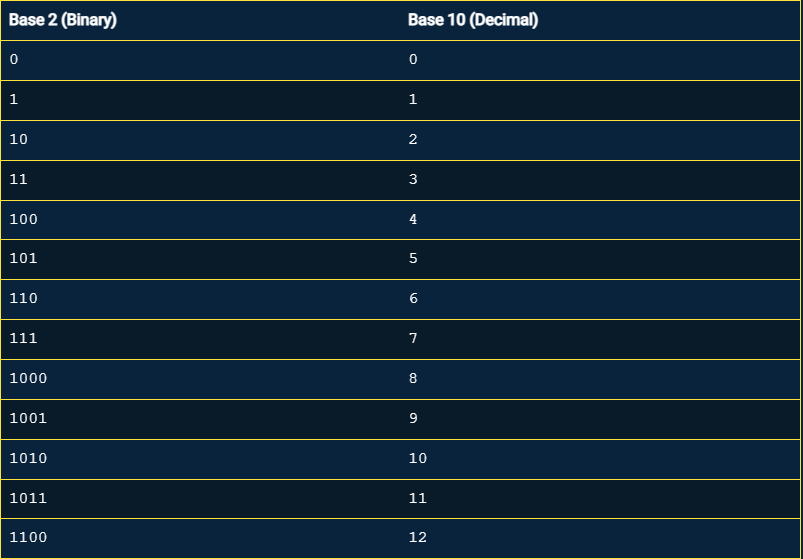
Hexadécimal

L’hexadécimal est un système de numération en base 16. Donc il existe 16 valeurs possibles pour chaque chiffre.

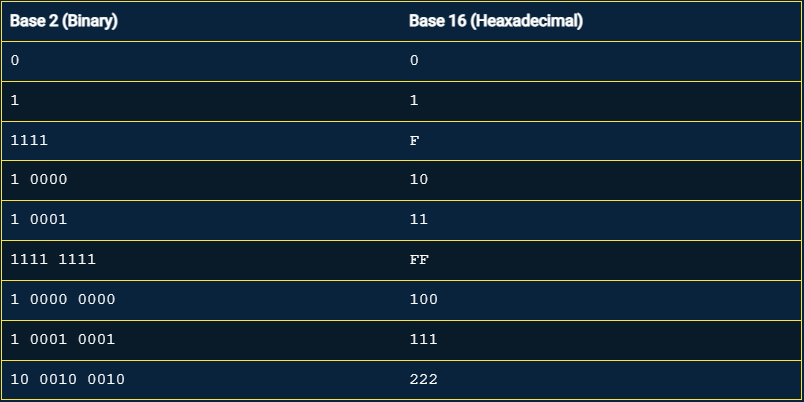
Voici un tableau qui compare des nombres exprimés dans les trois systèmes de numération : base 2, base 10 et base 16.

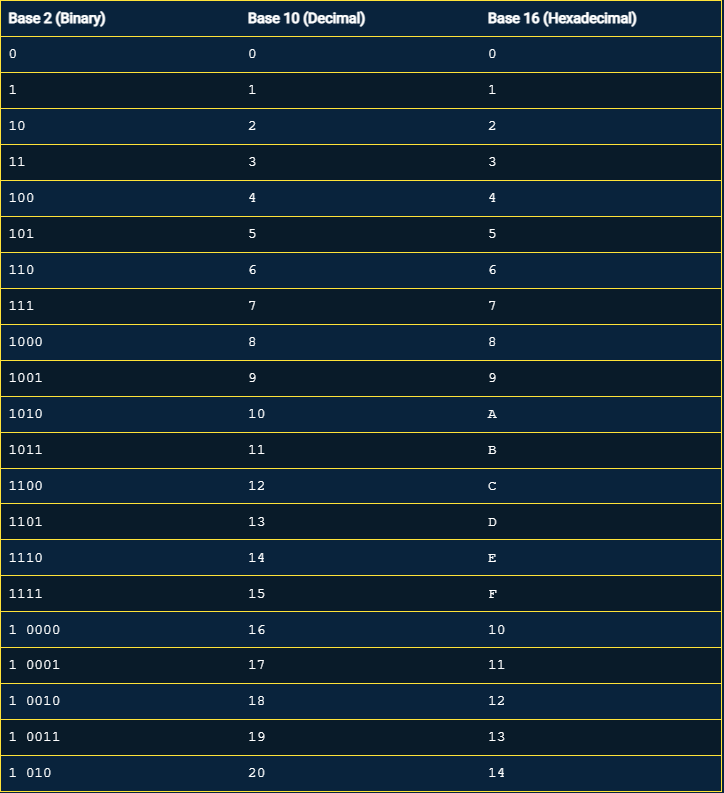
L’hexadécimal est populaire dans le monde des ordinateurs car il se traduit facilement en binaire. Chaque chiffre hexadécimal est traduit avec 4 chiffres binaires.

Préfixes

Les ordinateurs utilisent en interne des multiples de 8 bits (8 bits = 1 octet), donc chaque octet peut être représenté par 2 digits hexadécimaux. C’est plus simple à manipuler que des longues séquences en binaire. Les langages de programmation se servent de préfixes pour différencier les systèmes de numération. Par exemple, en langage C , le préfixe b représente le binaire et 0x est relatif à l’hexadécimal :

Notez que les zéros au début ne sont pas obligatoires (0b00000001 est identique à 0b1 et 0x01 est identique à 0x1). Ils sont utilisés pour faciliter la lecture selon le contexte.

En résumé, un système de numération différent de la base 10 que nous connaissons est aisé à comprendre à partir du moment où les principes sont compris. Vous pourriez conclure que le système décimal est meilleur que le binaire car il utilise moins de chiffres pour représenter un nombre ; ce raisonnement aboutirait à la conclusion que l’hexadécimal est meilleur que le décimal. En réalité nous aimons le décimal car nous avons l’habitude de l’utiliser et que tout le monde s’en sert.

Traduction française